Aufgabenblatt 03a

Arrays and Simulation		PI-1 2008/09

This assignment is designed to train you in two aspects of Java programming: (1) to work with arrays, and (2) to use computer simulation for studying simple scientific questions such as the birthday paradoxon.


Assignment #1:   Sieve of Eratosthenes (UE)

a) Write a Java program PrimeSieve.java that computes all prime numbers up to a given number N, using the  "Sieve of Eratosthenes" method. The number N can be provided to the program as a command line argument.

Sieve of Eratosthenes:

  1. Consider a contiguous list of numbers from 2 to some maximum N (see picture).
    (Implementation idea: Create a sufficiently long array of boolean values; initialize all elements to     true. This array represents the list of numbers as follows: If the value stored in the array at index [i] is true, then the number i is considered to be in the list; but if the value at that index is false, then number i has been removed from the list)

  2. Strike off all multiples of 2 greater than 2 from the list (i.e. in the array, set all those elements to false that have an index that is greater than 2 and is a multiple of 2)

  3. The next highest, uncrossed off number in the list is a prime number.
    Strike off all multiples of this number from the list. (Optimization: The crossing-off of multiples can be started at the square of the number, as lower multiples have already been crossed out in previous steps).

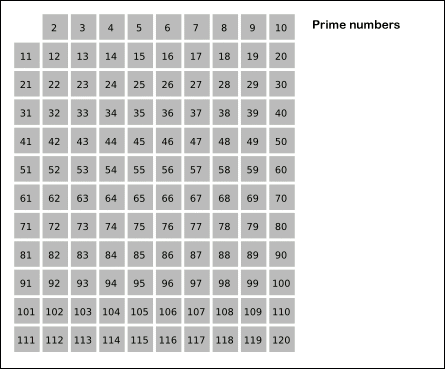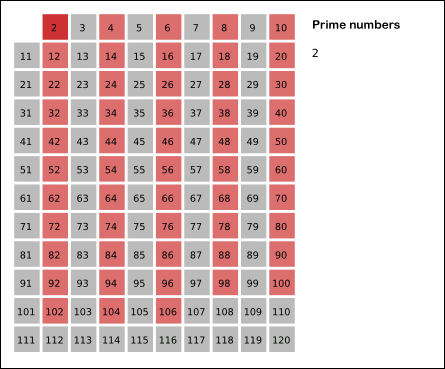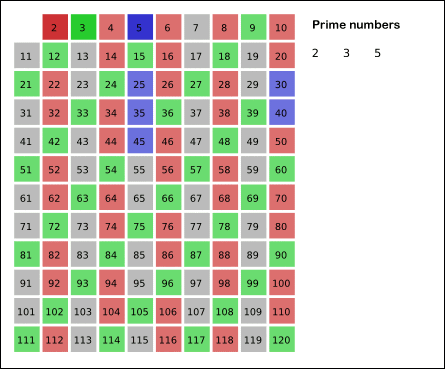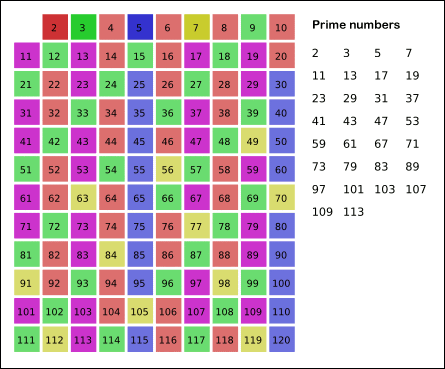
  4. Repeat steps 3 and 4 until you reach a number greater than or equal to the square root of the highest number in the list, all the numbers remaining in the list are prime.

Example:
% java PrimeSieve 6
 2
 3
 5

b) Write a Java program Prime.java that computes the first N prime numbers using the "Sieve of Eratosthenes". The number N can be provided to the program as a command line argument.

Example:
% java Prime 6
2
3
5
7
11
13
 

Be prepared to explain the following files in class (we recommend that you bring notes or a printout with you): PrimeSieve.java and Prime.java.

Concepts: one-dimensional arrays. Difficulty: low-medium.  


Assignment #2:   Banner (UE,PR) 10 points

Write a program Banner.java that prints its command line argument using seven rows of hash signs (#) like the one below. For simplification, we assume that the command line argument contains only numbers.

% java Banner 0815

  ###    #####     #    #######
 #   #  #     #   ##    #      
#     # #     #  # #    #      
#     #  #####     #    ###### 
#     # #     #    #          #
 #   #  #     #    #    #     #
  ###    #####   #####   #####

The following file might be useful for your solution: Numbers.java

Be prepared to explain the following files in class (we recommend that you bring notes or a printout with you): Banner.java
What to submit. Submit the file Banner.java to Goya.

Concepts: Multi-dimensional arrays. Difficulty: medium.

Assignment #3:   Matrix-Multiplication (UE,PR) 10 points

Schreiben Sie ein Programm MatrixMult.java, das von der Standard-Eingabe zwei Matrizen einliest, deren Matrix-Produkt berechnen und das Ergebnis ausgibt. Die Angaben zur Dimension der Matrizen imax, rmax und jmax  werden dem Programm als Kommandozeilen-Argumente übergeben.

Wie multipliziert man zwei Matrizen A and B?

Beispiel:

 

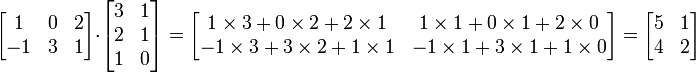
Beispiel.

% java MatrixMult 2 3 2

 1 0 2
-1 3 1

3 1
2 1
1 0

Output:
5.0 1.0
4.0 2.0

Be prepared to explain the following files in class (we recommend that you bring notes or a printout with you): MatrixMult.java
What to submit. Submit the file MatrixMult.java to Goya.

Concepts: 2-dimensional arrays (working with indices), StdInput. Difficulty: low.

Assignment #4:   Birthday Paradoxon (UE)

Wie groß ist die Wahrscheinlichkeit, dass von r zufällig in einem Raum befindlichen Leuten zwei am gleichen Tag Geburtstag haben? (Egal an welchem!)

Ermitteln Sie mit Hilfe einer Monte-Carlo-Simulation in Java (analog zum aus der VL bekannten Problem Gambler‘s Ruin) näherungsweise die Anzahl der nötigen  Personen, um mit einer Wahrscheinlichkeit von 0.5 (0.9) mindestens zwei Personen  mit Geburtstag am gleichen Tag (einer von 365 möglichen) zu erhalten. Auf was müssen Sie in der Umsetzung achten, um valide Ergebnisse zu erhalten (Tipp: Sie können nicht nur ein Experiment simulieren, sondern mehrere)?

Be prepared to explain the following files in class (we recommend that you bring notes or a printout with you): Birthday.java

Concepts: Simulation, statistical analysis. Difficulty: medium-high.

Assignment #5:   Drunkard's walk (UE)

A drunkard begins walking aimlessly, starting at a lamp post. At each time step, the drunkard forgets where he or she is, and takes one step at random, either north, east, south, or west, with probability 25%. How far will the drunkard be from the lamp post after N steps?
 

  • Write a program RandomWalker.java that takes a command-line argument N and simulates the motion of a random walker for N steps. After each step, print the location of the random walker, treating the lamp post as the origin (0, 0). Also, print the square of the distance from the origin.

    Extra credit: Visualize the path of the drunkard, similar to the picture above.

    % java RandomWalker 10             % java RandomWalker 20
(0, 0)                            (0, 0)Random walk in the plane
(0, -1)                           (0, 1)
(0, 0)                            (-1, 1)
(0, 1)                            (-1, 2)
(0, 2)                            (0, 2)
(-1, 2)                           (1, 2)
(-2, 2)                           (1, 3)
(-2, 1)                           (0, 3)
(-1, 1)                           (-1, 3)
(-2, 1)                           (-2, 3)
(-3, 1)                           (-3, 3)
squared distance = 10             (-3, 2)
                                  (-4, 2)
                                  (-4, 1)
                                  (-3, 1)
                                  (-3, 0)
                                  (-4, 0)
                                  (-4, -1)
                                  (-3, -1)
                                  (-3, -2)
                                  (-3, -3)
                                  squared distance = 18

     

  • Write a program RandomWalkers.java that takes two command-line argument N and T. In each of T independent experiments, simulate a random walk of N steps and compute the squared distance. Output the mean squared distance (the average of the T squared). 
    % java RandomWalkers 100 100000         % java RandomWalkers 400 100000
mean squared distance = 100.15086       mean squared distance = 401.22024

% java RandomWalkers 100 100000         % java RandomWalkers 800 100000
mean squared distance = 99.95274        mean squared distance = 797.5106

% java RandomWalkers 200 100000         % java RandomWalkers 1600 100000
mean squared distance = 199.57664       mean squared distance = 1600.13064

     

  • As N increases, we expect the random walker to end up further and further away from the origin. But how much further? Use RandomWalkers to formulate a hypothesis as to how the mean squared distance grows as a function of N. Use T = 100000 trials to get a sufficiently accurate estimate.

Be prepared to explain the following files in class (we recommend that you bring notes or a printout with you): RandomWalkers.java
What to submit. Submit the file RandomWalkers.java to Goya.

Concepts: Simulation, statistical analysis, arrays. Difficulty: medium.

Assignment #6:   Dice and the Gaussian distribution (UE)

Write a program TenDice.java that takes a command-line argument N, and flips 10 fair dices, N times. Use an array to tabulate the number of times each possible total (between 10 and 60) occurs. Then print out a text histogram of the results, as illustrated below. 

% java TenDice 1000
10: 
11: 
12: 
13: 
14: 
15: 
16: 
17: 
18: *
19: ****
20: 
21: ***
22: ******
23: ********
24: ****************
25: *************
26: **********
27: *********************************
28: ****************************************
29: *********************************
30: ***************************************************
31: *****************************************************************
32: ********************************************************
33: **************************************************************************************
34: ***********************************************************
35: *********************************************************************
36: ***********************************************************************************
37: **************************************************************
38: *****************************************************************
39: ***************************************
40: *****************************************************
41: ************************************
42: ****************************
43: ************************
44: ************************
45: *********
46: ***********
47: *******
48: ***
49: **
50: 
51: 
52: *
53: 
54: 
55: 
56: 
57: 
58: 
59: 
60:

Remark: a classic result from probability theory asserts that the shape of the resulting histogram is well-approximated by the ubiquitous bell curve (Gaussian distribution).

 

Be prepared to explain the following files in class (we recommend that you bring notes or a printout with you): TenDice.java
What to submit. Submit the file TenDice.java to Goya.

Concepts: Simulation, statistical analysis, arrays. Difficulty: low.