Lernziele: Backtracking (with optimization constraint).

Das Rucksackproblem (Knapsack) ist ein Optimierungsproblem der Kombinatorik. Aus einer Menge von Objekten, die jeweils ein Gewicht und einen Nutzenwert haben, soll eine Teilmenge ausgewählt werden, deren Gesamtgewicht eine vorgegebene Gewichtsschranke nicht überschreitet. Unter dieser Bedingung soll der Nutzenwert der ausgewählten Objekte maximiert werden.

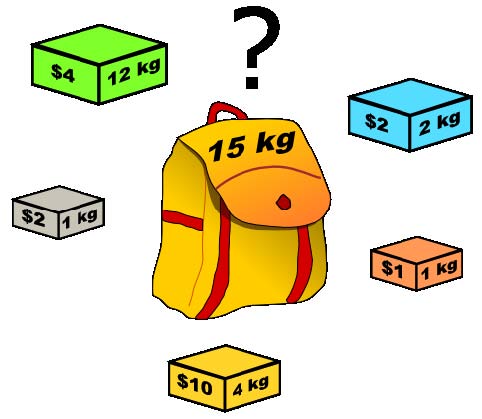
Abbildung. Welche der Gewichte können in den Rucksack mit Maximallast von 15 kg gepackt werden, so dass der Geldwert maximal wird? (Lösung in diesem Fall: Alle Gewichte außer dem schwersten einpacken.) Quelle: Wikipedia.org

Problemformulierung

Gegeben sind eine endliche Menge von Objekten U. Durch eine Gewichtsfunktion w und der Nutzenfunktion v wird den Objekten ein Gewicht und ein Nutzenwert zugeordnet: w:U→R,  v:U → R
Des Weiteren gibt es eine vorgegebene Gewichtsschranke: B Î R.
Gesucht ist eine Teilmenge K Í R, die die Bedingung ∑ w(u) ≤ B einhält und die Zielfunktion maximiert:∑ v(u)

Aufgabe

Implementieren Sie das Rucksackproblem mit Hilfe eines Java-Programms. Verwenden Sie Rekursion! Diskutieren Sie Ihre Lösung hinsichtlich der Komplexität. Können Sie auch eine iterative Lösung finden? Wenn ja, welche (->Java-Programm)?

Hinweise

Die Beschreibung findet sich unter de.wikipedia.org/wiki/Rucksackproblem. Die Kapazität C des Rucksacks ist ein frei wählbarer Parameter. Sowohl die Gewichte w der Gegenstände als auch deren Wertigkeit v sind konfigurierbar. Beide sollen in einem Feld verwaltet werden.