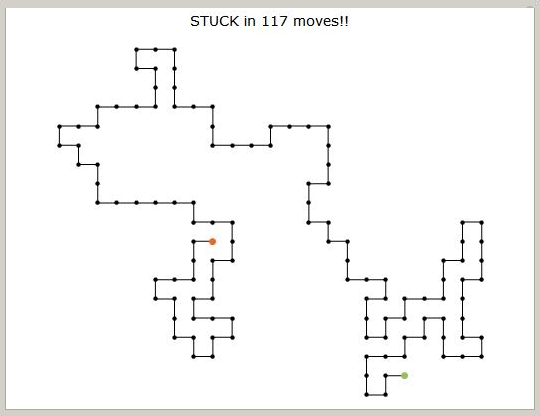
2D Self-Avoiding Random Walk.

Given a 2-dimensional grid of size NxN, start at an arbitrary position (x,y) with 0<x<N, 0<y<N. The grid size is given as command line argument e.g.:

java SelfAvoidingWalk 100

At each simulation step, go to all possible directions left/right/up/down with eaqual probability. Never accept a step to positions which has been touched in the past. Also do not step on to the border (x=0 or x=N)or (y=0 or y=N). Continue the walk until there is no further option to go.

Draw a line along the path. Draw a black point for the intermediate states, a larger green one for the start point and a red one for the final destination. Print the number of moves as Text into the graphics.

Assignment

Write a program SelfAvoidingWalk.java to simulate and animate a 2D self-avoiding random walk. Print out its length (i.e. the number of simulation steps until the SAW intersected with itself).

Submit the file SelfAvoidingWalk.java to Goya.

Interesting question. Among all self-avoiding walks (SAW) of length N, what is the average distance from the origin? How long does it take (i.e. how many simulations steps) until the SAW reaches a certain length L? Practically nothing is known rigorously about these questions, so numerical simulation is the best recourse. Here's an article "How_to_Avoid_Yourself" from the American Scientist