In 1687 Sir Isaac Newton formulated the principles governing the motion of two particles under the influence of their mutual gravitational attraction in his famous Principia. However, Newton was unable to solve the problem for three particles. Indeed, in general, systems of three or more particles can only be solved numerically. Write a program to simulate the motion of N particles, mutually affected by gravitational forces, and animate the results. Such methods are widely used in cosmology, semiconductors, and fluid dynamics to study complex physical systems. Scientists also apply the same techniques to other pairwise interactions including Coulombic, Biot-Savart, and van der Waals.

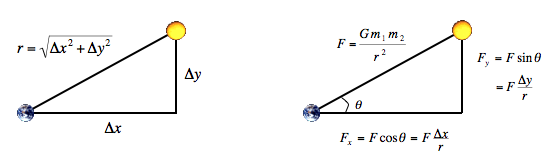
The physics. We review the equations governing the motion of the particles according to Newton's laws of motion and gravitation. Don't worry if your physics is a bit rusty; all of the necessary formulas are included below. We'll assume for now that the position (r_x, r_y) and velocity (v_x, v_y) of each particle is known. In order to model the dynamics of the system, we must know the net force exerted on each particle.

• Pairwise force. Newton's law of universal gravitation asserts that the strength of the gravitational force between two particles is given by the product of their masses divided by the square of the distance between them, scaled by the gravitational constant G (6.67 × 10^-11 N m² / kg²). The pull of one particle towards another acts on the line between them. Since we are using Cartesian coordinates to represent the position of a particle, it is convenient to break up the force into its x and y components (F_x, F_y) as illustrated below.
• Net force. The principle of superposition says that the net force acting on a particle in the x or y direction is the sum of the pairwise forces acting on the particle in that direction. (the force is attractive)
   
• Acceleration. Newton's second law of motion postulates that the accelerations in the x and y directions are given by: a_x = F_x / m, a_y = F_y / m.

The numerics.  We use the leapfrog finite difference approximation scheme to numerically integrate the above equations: this is the basis for most astrophysical simulations of gravitational systems. In the leapfrog scheme, we discretize time, and update the time variable t in increments of the time quantum Δt. We maintain the position and velocity of each particle, but they are half a time step out of phase (which explains the name leapfrog). The steps below illustrate how to evolve the positions and velocities of the particles.

1. Calculate the net force acting on each particle at time t using Newton's law of gravitation and the principle of superposition.
    
2. For each particle:
    
   1. Calculate its acceleration (a_x, a_y) at time t using its force at time t and Newton's second law of motion.
       
   2. Calculate its velocity at time t + Δt / 2 by using its acceleration at time t and its velocity (v_x, v_y) at time t - Δt / 2. We assume the acceleration remains constant in this interval: the updated velocity is (v_x + Δt a_x, v_y + Δt a_y).
       
   3. Calculate its position at time t + Δt by using its velocity at time t + Δt / 2 and its position at time t. We assume the velocity remains constant in the interval from t to t + Δt: the resulting position is (r_x + Δt v_x, r_y + Δt v_y). Note that because of the leapfrog scheme, the constant velocity we are using is the one estimated at the middle of the interval rather than either of the endpoints.
       
3. Draw each particle.

Creating an animation. Draw each particle at its current position using standard draw, and repeat this process at each time step. By displaying this sequence of snapshots (or frames) in rapid succession, you will create the illusion of movement. After each time step (i) draw the background image starfield.jpg, (ii) redraw all the bodies in their new positions, and (iii) control the animation speed using StdDraw.show().

Input format. The input is a text file that contains the information for a particular universe. The first value is an integer N which stores the number of particles. The second value is a real number R which represents the radius of the universe: assume all particles will have coordinates that remain between -R and R. Finally, there are N rows, and each row contains 6 elements. The first two are the x and y coordinates of the initial position; the second two are the x and y coordinates of the initial velocity; the third is the mass; the last is a String that is the name of an image file used to display the particle. As an example, the file planets.txt contains data for our solar system (in SI units)  in the format:
# of planets
Radius of solar system
x(0) y(0) vx(-Dt/2) vy(-Dt/2) planet_mass planet_img
...

5
2.50e11
1.496e11 0.000e00 0.000e00 2.980e04 5.974e24 earth.gif
2.279e11 0.000e00 0.000e00 2.410e04 6.419e23 mars.gif
5.790e10 0.000e00 0.000e00 4.790e04 3.302e23 mercury.gif
0.000e00 0.000e00 0.000e00 0.000e00 1.989e30 sun.gif
1.082e11 0.000e00 0.000e00 3.500e04 4.869e24 venus.gif

All files together are available as nbody.zip.

Your program.   Write a program NBody.java that reads in the universe from standard input using StdIn, simulates its dynamics using the leapfrog scheme described above, and animates it using our StdDraw. Maintain several arrays to store the data. To make the computer simulation, write an infinite loop that repeatedly updates the position and velocity of the particles. When plotting, consider using StdDraw.setXscale(-R, +R) and StdDraw.setYscale(-R, +R) to scale the physics coordinates to the screen coordinates. Compiling and executing your program. To compile your program from the command-line, type:

% javac NBody.java

in your Terminal application. To run your program from the command-line on the input file planets.txt, redirect the file to standard input:

% java NBody < planets.txt

It produces an animation like the following movie.

Submit the file NBody.java to Goya.

Optional finishing touch. For a finishing touch, play the theme to 2001: A Space Odyssey using StdAudio and the file 2001.mid. It's a one-liner using the method StdAudio.play().

Challenge for the bored. There are limitless opportunities for additional excitement and discovery here. Try adding other features, such as supporting elastic or inelastic collisions. Or, make the simulation three-dimensional by doing calculations for x, y, and z coordinates, then using the z coordinate to vary the sizes of the planets. Add a rocket ship that launches from one planet and has to land on another. Allow the rocket ship to exert force with consumption of fuel.

Credits: This programming assignment was taken from http://www.cs.princeton.edu/courses/archive/spr01/cs126/assignments/nbody.html (copyright by Robert Sedgewick)